In diesem Artikel beschreibe ich, wie die Kreiszahl Pi mittels Polygone möglichst genau berechnet werden kann. Für die Implementierung habe ich die Programmiersprache Python verwendet.
Kurze Einführung: Was ist Pi?
Pi (auch bekannt als Kreiszahl, griechisch Zeichen: π) ist eine mathematische Konstante, welche das Verhältnis eines Kreisumfangs zu seinem Durchmesser darstellt. Ein Kreis mit dem Durchmesser 1 hat den Umfang Pi, also ca. 3,1415. Eine andere gleichwertige Definition beschreibt Pi über die Fläche A eines Kreises mit dem Radius r: A = π * r2. Diese Definition wird im weiteren Verlauf des Artikels nochmal benötigt.
Pi ist eine irrationale Zahl - eine Darstellung als Bruch zweier ganzer Zahlen ist also nicht möglich. Da Pi sogar transzendent ist, kann die Zahl nicht mit ganzen Zahlen, Brüchen und Wurzeln dargestellt werden.
Es existieren diverse Methoden um sich Pi anzunähern, auf die ich in diesem Artikel aber nicht näher eingehen werde. Verwenden möchte ich Polygone zur Berechnung einer Kreisoberfläche um so eine Annäherung von Pi zu erhalten.
Wie helfen Polygone zur Berechnung von Pi?
Ein Polygon ist eine geometrische Figur, welche auch als Vieleck bekannt ist. Erstellt wird ein Polygon, indem mehrere Punkte durch Kanten miteinander verbunden werden. Es existieren diverse Polygon-Klassifikationen, welche das Verhalten der Vielecke näher beschreiben. Für die Berechnung von Pi sind regelmäßig konvexe Polygone notwendig. Bei regelmäßig konvexen Polygonen sind zum einen alle Kanten (die Linien zwischen zwei Punkten) gleich lang, zum anderen besitzt jede Seite den gleichen Innenwinkel α.
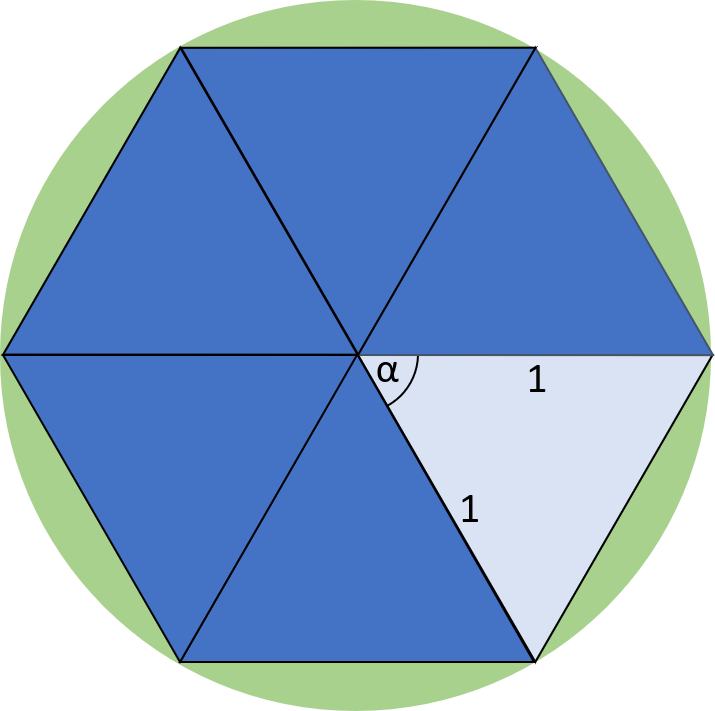Ein Polygon mit n Ecken lässt sich auf Grund der regelmäßig-konvexen Eigenschaft in n gleiche Dreiecke unterteilen. Summiert man nun die Flächen aller Dreiecke erhält man die Fläche des gesamten Polygons.
Der Winkel αn sowie die Fläche An eines n-eckigen Polynoms lassen sich wie folgt berechnen, wenn der Abstand vom Mittelpunkt bis zu einer beliebigen Ecke des Polynoms 1 ist:
αn = 360°/n
An = n * (1/2 * sin(αn))
Das 6-eckige Polynom oben im Bild hat zum Beispiel die Fläche A6:
A6 = 6 * (1/2 * sin(360°/6)) ≈ 2,59807
Wird ein solches Polygon nun in einen Kreis mit dem Radius 1 gelegt, wird ein Teil der Kreisfläche bedeckt. Die Fläche FKreis eines Kreises mit dem Radius r ist das Produkt von Pi mit r2. Da der r und somit auch r2 im Beispiel oben 1 sind ist die Fläche FKreis gleich Pi.
Erhöht man die Zahl der Ecken nähert sich die Fläche des Polygons immer näher der Fläche des Kreises an:
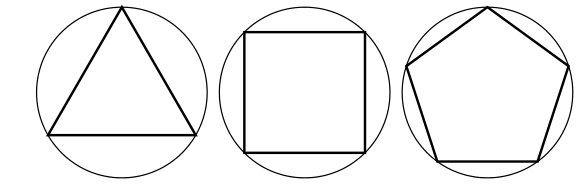
Würde man die Anzahl der Ecken n nun gegen ∞ laufen lassen, könnte man "den exakten Wert Pi" ermitteln. Es wird im weiteren Verlauf des Artikels aber klar, dass schon ein Polygon mit "nur" 1.000 Ecken als ziemlich exakte Annäherung ausreicht.
Berechnen von Pi mit Python
Methoden zur Berechnung
Als Vorbereitung habe ich drei Funktionen implementiert, die zum einen die Fläche eine n-eckigen Polygons berechnet, und zum anderen die Ergebnisse in der Konsole bzw. in einem Plot darstellen. In der Konsolenausgabe wird neben der errechneten Fläche auch die absolute und prozentuale Abweichung zum deutlich genauerem math.pi dargestellt.
import math
from matplotlib import pyplot
def berechne_flaeche_polygon(ecken):
winkel_deg = 360 / ecken
winkel_rad = math.radians(winkel_deg)
flaeche_dreieck = 0.5 * math.sin(winkel_rad)
flaeche_polygon = ecken * flaeche_dreieck
return flaeche_polygon
def print_flaeche(ecken):
flaeche = berechne_flaeche_polygon(ecken)
differenz = math.pi - flaeche
print("Fläche Polygon mit {:9} Ecken: {:.15f}\t\tAbweichung von Pi: {:.20f} ({:8.5f} %)".format(
ecken, flaeche, differenz, 100 * differenz / math.pi)
)
def plot_flaechen(start, end):
flg, ax = pyplot.subplots()
list_x = range(start, end+1)
list_y = []
for x in list_x:
list_y.append(berechne_flaeche_polygon(x))
ax.plot(list_x, list_y)
ax.set(xlabel="Anzahl Ecken Polygon",
ylabel="Fläche Polygon",
title="Fläche Polygon (Ecken: {}..{})".format(start, end))
pyplot.show()1. Anlauf: Polygone mit wenigen Ecken
Im ersten Anlauf habe ich die Fläche der Polygone mit 3 bis 20 Ecken errechnet und anschließend ausgegeben bzw. grafisch dargestellt:
for n in range(3, 21):
print_flaeche(n)
plot_flaechen(3, 20)Das Resultat in der Konsole (hier verkürzt dargestellt) zeigt deutlich, dass die Abweichungen bei Polygonen mit wenig Ecken mit fast 60% sehr hoch sind. Aber schon bei einem 20-eckigen Polygon nehmen die Abweichungen stark ab:
Fläche Polygon mit 3 Ecken: 1.299... Abweichung von Pi: 1.842... (58.65033 %)
Fläche Polygon mit 4 Ecken: 2.000... Abweichung von Pi: 1.141... (36.33802 %)
...
Fläche Polygon mit 19 Ecken: 3.084... Abweichung von Pi: 0.056... ( 1.81270 %)
Fläche Polygon mit 20 Ecken: 3.090... Abweichung von Pi: 0.051... ( 1.63684 %)
Besonders deutlich wird dies beim Betrachten der grafischen Darstellung, bei der die berechnete Fläche gegen die Anzahl der Ecken dargestellt wird:
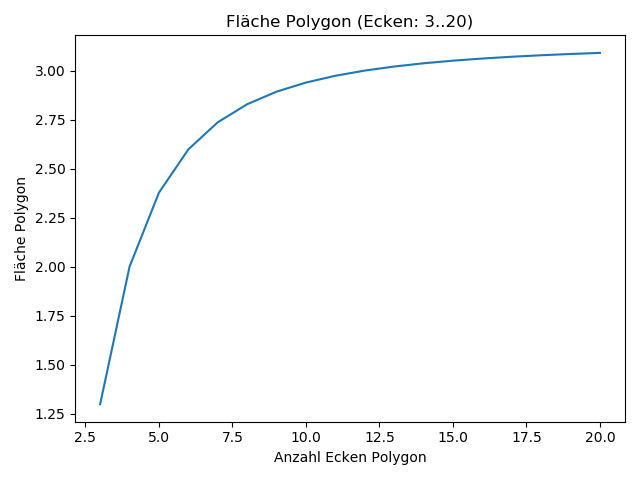
2. Anlauf: Polygone mit vielen Ecken
Das genaueste Ergebnis meiner Pi-Annäherung mit ~3,090 aus dem 1. Anlauf war mit einer Abweichung von ~1,6% zwar relativ genau, allerdings ist durch die Verwendung von mehr als nur 20 Ecken auch ein deutlich genauerer Wert möglich. Im 2. Anlauf habe ich daher die Fläche der Polygone mit 10n (mit 3≤n≤8) Ecken berechnet:
for e in range(3, 9):
print_flaeche(10 ** e)
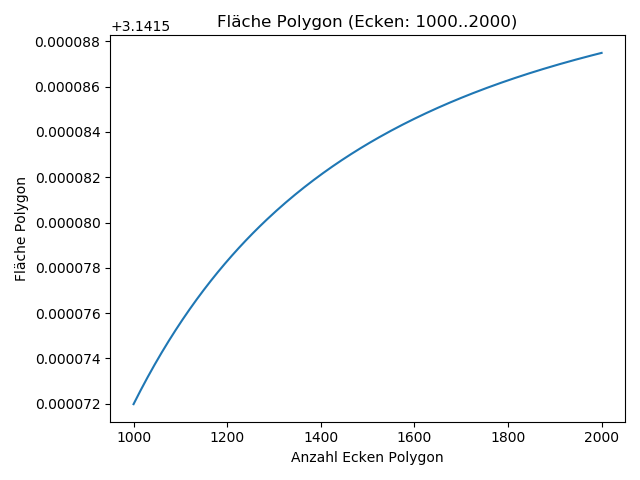
plot_flaechen(10 ** 3, 10 ** 8)Die Fläche eines Polygons mit 108 (also 100.000.000) Ecken war so genau, dass die Abweichung von math.pi nur 0,00000000000000222045 beträgt. Für den praktischen Gebrauch ist die Fläche des 1000-eckigem Polygons mit einer Abweisung von nur 0,00066% aber genau genug.
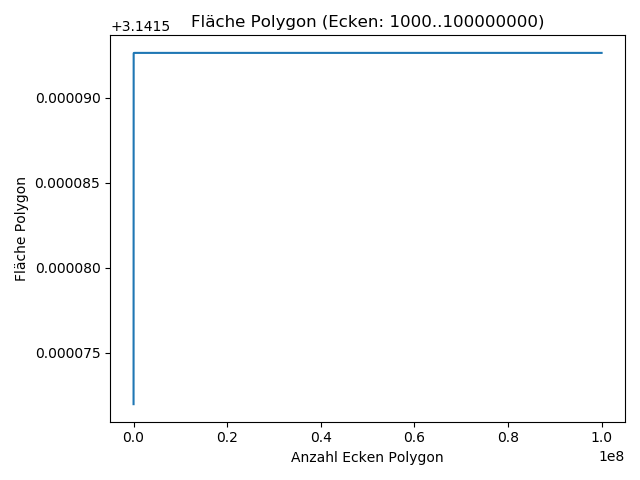
Im Plot oben ist die Fläche der Polygone mit 103 bis 108 Ecken dargestellt. Es wird deutlich, dass die Änderungen schnell so gering werden, dass diese nur noch als horizontale Linie zu erkennen sind. Betrachtet man einen kleinen Ausschnitt dieser scheinbar horizontalen Linie fällt jedoch auf, dass es noch immer Änderungen der Fläche gibt. Erhöht man die Anzahl der Ecken werden diese Änderungen immer geringer ausfallen - verschwinden werden diese jedoch nie:
