In der Uni-Veranstaltung "Algorithmen und Datenstrukturen" wurden wir in Themen wie Rekursion, Listen, Bäume, Problemklassen sowie Such- bzw. Sortierverfahren eingeführt.
Dabei haben wir diverse Sortierverfahren kennengelernt, die auf Grund ihrer unterschiedlichen Komplexitätsklassen unterschiedlich effizient Datenmengen sortieren können. Ich habe mich für diese Differenzen so sehr interessiert, dass ich spontan einige wichtige Sortier-Algorithmen und Python implementiert und verglichen habe.
Eine Liste weiterer wissenschaftlicher Arbeiten, sowie deren Nutzungsbedingungen, ist hier verlinkt.
In diesem Blog-Artikel werde ich mein Test-Projekt, sowie die diversen Sortier-Algorithmen grundsätzlich vorstellen, und auch vergleichen.
Einführung in mein Test-Projekt
Mein Python-Projekt besteht aus zwei Modulen: eins beinhaltet die eigentlichen Sortier-Klassen, das andere vergleicht schließlich die verschiedenen Algorithmen.
Jeder Sortier-Algorithmus ist in einer eigenen Klasse implementiert, die alle von der Basisklasse _Template erben. Diese implementiert Methoden zum Vergleichen und Austauschen von Listen-Feldern, da diese Routinen von fast jedem Sortier-Verfahren genutzt werden. Im Konstruktor der _Template-Klasse kann optional eine eigene Vergleichs-Funktion, sowie eine Key-Funktion angegeben werden. Die Vergleichs-Funktion mit zwei Parametern p1 und p2 gibt 0 zurück, wenn beide Parameter identisch sind, eine Zahl kleiner 0, wenn p2>p1, und eine Zahl größer als 0, wenn p1>p2. Mit Hilfe der Key-Funktion kann festgelegt werden, welches Attribut eines zu sortierenden Objektes genutzt werden soll. Außerdem kann angegeben werden, dass die Liste absteigend, statt aufsteigend sortiert werden soll.
_defaultCompare = lambda x, y: x - y
_defaultKey = lambda a: a
class _Template(object):
def __init__(self, compare=_defaultCompare, key=_defaultKey, ascending=False):
## ...
class BestSort(_Template):
## ...
class Person(object):
def __init__(self, name, alter):
self.name = name
self.alter = alter
personen = [Person("Max", 22), Person("Karl", 54), Person("Nicole", 34)]
nachAlterSortiert = BestSort(key=lambda a: a.alter).sort(personen)
nachNamenSortiert = BestSort(key=lambda a: a.name.upper(), compare=lambda x,y: (0 if x==y else (1 if x>y else -1))).sort(personen)
Implementiert habe ich drei primitive Algorithmen (Bubble Sort, Selection Sort & Insertion Sort) und drei komplexe Algorithmen (Heap Sort, Merge Sort & Quick Sort).
Außerdem habe ich ein Vergleichs-Skript erstellt, dass die einzelnen Algorithmen mit verschieden vielen Test-Einträgen vergleicht.
Im Kopf des Vergleich-Moduls kann der Vergleich konfiguriert werden. Es kann angegeben werden, mit wie vielen Elementen die einzelnen Algorithmen getestet werden sollen (Standard mit 22 - 222 Elementen). Zudem kann festgelegt werden, wie häufig ein Algorithmus mit einer Menge an Daten getestet werden soll. Es wird dann der Mittelwert aller Ergebnisse errechnet.
Für jeden Algorithmus, der verglichen werden soll, kann zudem ein maximaler Exponent angegeben werden - der Bubble Sort wird beispielsweise mit maximal 213 Elementen aufgerufen, da sich die Laufzeit des Vergleich-Skripts sonst auf mehrere Jahre erhöhen würde...
START_E = 2 # 2^2 = 4
MAX_E = 22 # 2^22 = 4.194.304
TRIES = 1
TOTEST = (
#(Class, Name, Max)
(BadAlgorithm, "BadAlgorithm", 3),
(BubbleSort, "BubbleSort", 12),
(SelectionSort, "SelectionSort", 13),
(InsertSort, "InsertSort", 14),
(HeapSort, "HeapSort", 19),
(MergeSort, "MergeSort", 22),
(QuickSort, "QuickSort", 22),
)Veröffentlicht habe ich den Quelltext meines Projektes auf github unter der MIT-Lizenz.
Beschreibung der Algorithmen
Unten findest du zu jedem Sortier-Algorithmus, den ich implementiert habe eine kurze Beschreibung der Funktionsweise. Zu den komplexeren Verfahren habe ich zum besseren Verständnis einige Grafiken erstellt.
Detailliertere Informationen und Beispiele wären für diesen Blog-Artikel jedoch zu viel, sind im Internet aber einfach zu finden.
Bad Algorithm
Der Bad Algorithm ist die wohl schlechteste Art und Weise eine Liste zu sortieren. Die Eingabe-Liste wird bei diesem Verfahren so lange zufällig gemischt, bis diese zufällig korrekt sortiert ist.
Im engsten Sinne ist dieses Verfahren jedoch gar kein Algorithmus, da nicht sichergestellt ist, dass dieser terminiert. Werden 8 Elemente sortiert ist der Algorithmus in meinem Beispiel normal nach weniger als 0,1 Sekunden abgeschlossen. Verdoppelt man die Anzahl der Elemente (also 16 Elemente) war nach 8 Stunden noch kein Ergebnis gefunden, sodass ich das Skript schließlich abgebrochen habe.
Bubble Sort
Beim Bubble Sort wird die Eingabe-Liste von links nach rechts "durchlaufen", wobei in jedem Step das ausgewählte Element mit seinem rechten Nachbarn verglichen wird. Ist das rechte Element kleiner als das Ausgewählt, werden beide Listen-Elemente getauscht. Wurden alle Listen-Elemente ein mal "abgegangen" ist das letzte Element in der Liste zwangsläufig das größte aller Listen-Einträge. Der Vorgang wird nun wiederholt, bis in einem Durchgang keine Elemente mehr getauscht wurden.
Dieses Sortier-Verfahren ist relativ einfach zu implementieren, wird jedoch wegen seiner relativ hohen Laufzeit nur selten eingesetzt. Einzig beim Sortieren einer Liste, die bereits fast sortiert ist, ist dieser Algorithmus effizient einsetzbar.

Selection Sort
Beim Selection Sort wird die Eingabe-Liste in zwei imaginäre Abschnitte aufgeteilt - einem sortierten und einem unsortierten Part, wobei der Unsortierte zu Beginn leer ist. Normalerweise wird am Anfang der Liste der sortierte, und am Ende der unsortierte Part gespeichert.
Im unsortiertem Bereich wird nun das kleinste Element gesucht (indem alle Elemente durchgangen werden) und mit dem ersten Element des sortierten Bereiches vertauscht, sodass sich der sortierte Bereich nach jedem Durchgang um ein Element vergrößert. Der Vorgang wird solange wiederholt, bis im unsortiertem Bereich nur noch ein Element vorhanden ist.

Insertion Sort
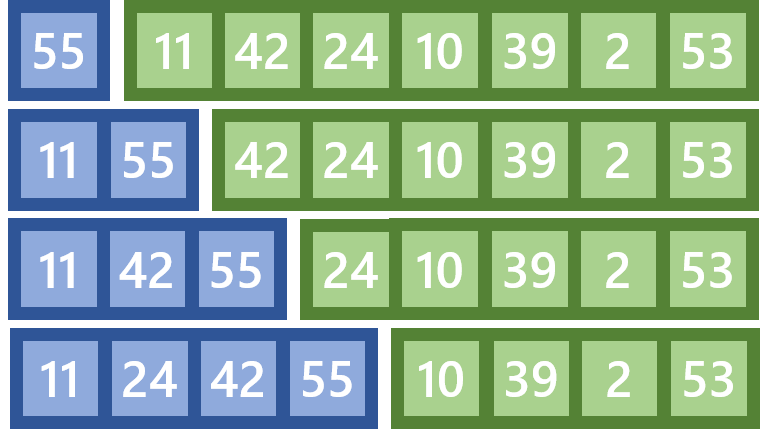
Der Insertion Sort funktioniert ähnlich wie der Selection Sort. Wieder ist die Liste in einen sortierten und einen unsortierten Bereich aufgeteilt. Es wird nun aber das erste Element aus dem unsortierten Bereich "genommen", und an die richtige Stelle im sortiertem Bereich eingefügt. Problematisch ist bei diesem Verfahren jedoch, dass nach dem Einfügen im Sortiertem Bereich alle folgenden Einträge verschoben werden müssen, was relativ aufwendig ist. Daher wird dieser Algorithmus nur selten eingesetzt.
Heap Sort
Der Heap Sort funktioniert deutlich komplizierter als die bisherigen Algorithmen. Zunächst wird die Eingabe-Liste in einen Heap umgewandelt. Ein Heap ist ein binärer Baum mit der Eigenschaft, dass die Kinder jedes Knotens kleiner als der Knoten selbst sind. Auf Grund dieser Eigenschaft ist das größte Element immer die Wurzel des Baumes. Ein Heap kann gut in Form einer Liste abgespeichert werden. Die Kinder eines Knotens mit dem Index i liegen dann - wie in der Grafik unten - bei 2*i+1 und 2*i+2. Knoten, die keine Kinder haben, werden als Blätter (hier in blau) bezeichnet.
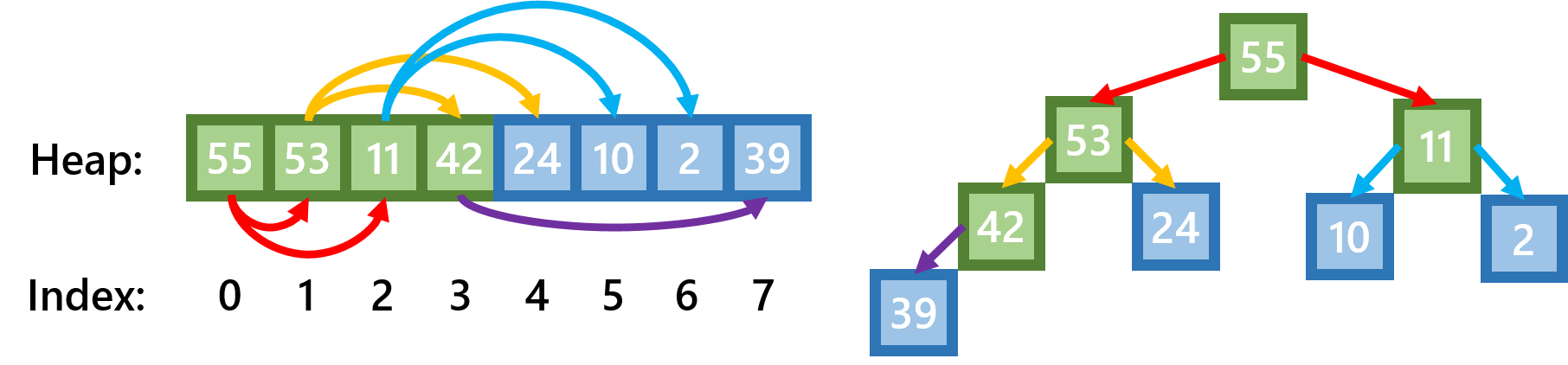
Um aus einer Liste eine Heap-Liste zu erstellen müssen alle Knoten, die keine Blätter sind von rechts nach links versickert werden (also hier die Indizes in dieser Reihenfolge: 3, 2, 1 und 0).
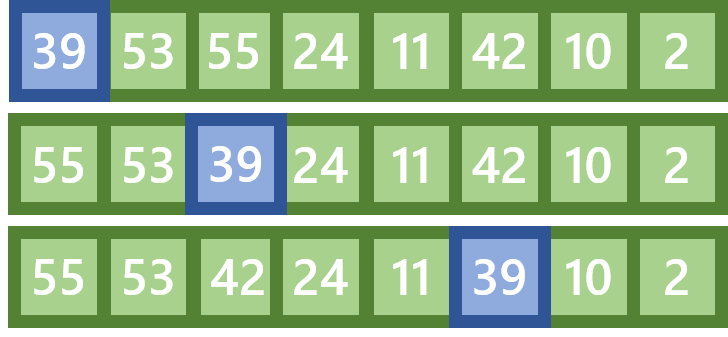
Beim Versickern eines Knotens wird der Wert dieses Knotens mit den Werten seiner Kinder verglichen. Ist einer seiner Kinder größer als er selbst, dann wird der Knoten mit dem größten seiner Kinder ausgetauscht, und der Vorgang wird für den Knoten, der nun eine Ebene nach unten verschoben wurde so lange wiederholt, bis der nicht mehr getauscht werden musste. In dem Beispiel unten wird zum Beispiel der Knoten mit dem Index 0 (Wert: 39) so tief wie möglich versickert:
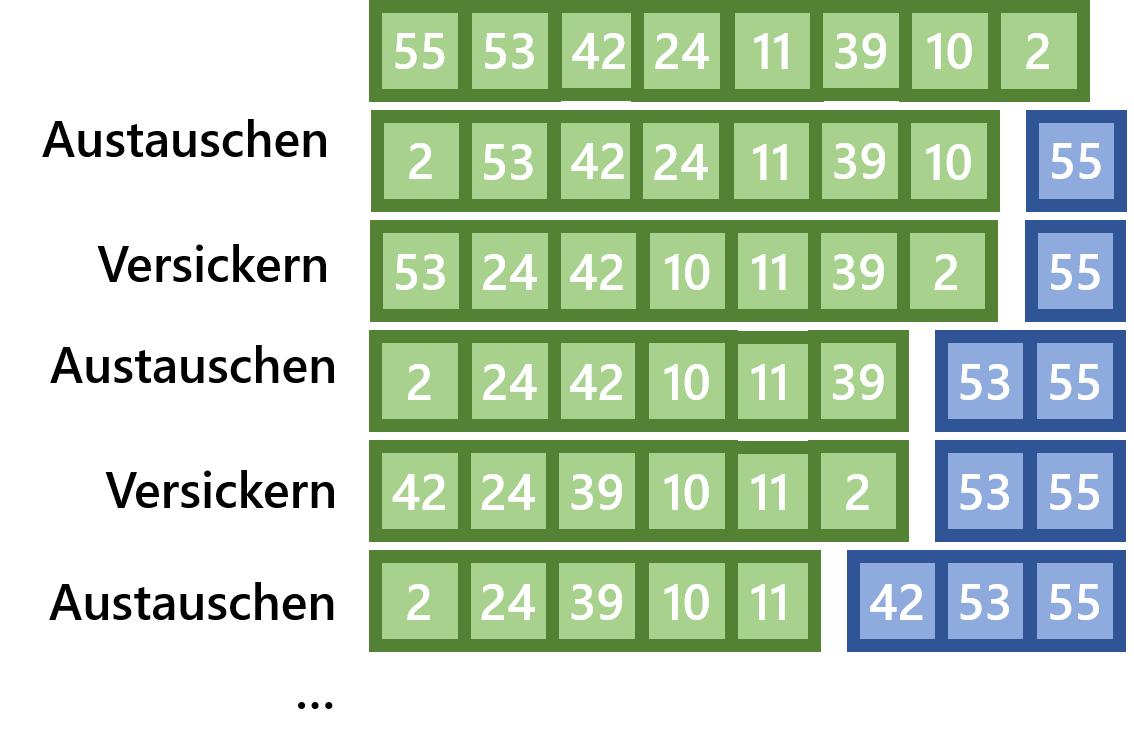
Wurde aus der Liste ein Heap erstellt, wird die Liste wieder in einem imaginären unsortierten Part (zu Beginn der Liste) und einen sortierten Part (am Ende der Liste) eingeteilt. Es wird dann immer das erste Element des unsortierten Parts mit dem Letzten getauscht, und die Grenzen für den Sortierten Part wird um eins erhöht. Anschließend wird das nun erste Element des unsortierten Parts wieder versickert, sodass aus diesem wieder ein Heap wird, und wieder das größte Element an erster Stelle steht.
Die ersten Steps des Heap Sort-Verfahrens habe ich hier grafisch dargestellt:
Merge Sort
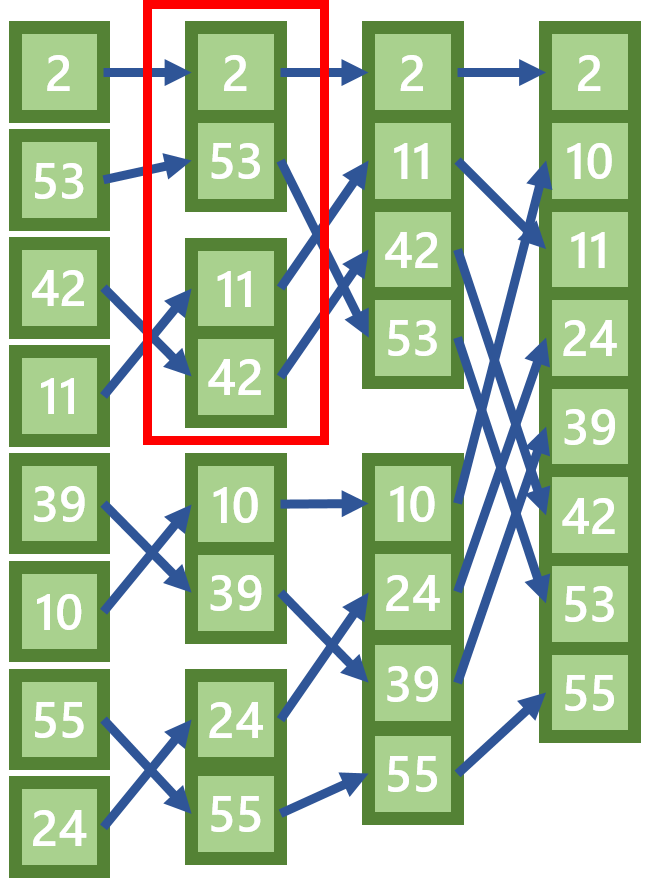
Das Merge Sort Verfahren ist ähnlich effizient wie das Heap Sort-Verfahren, jedoch (meiner Meinung nach) deutlich einfacher zu verstehen. Die Liste wird beim Merge Sort in verschiedene imaginäre Bereiche eingeteilt (in der Grafik unten durch Lücken dargestellt). Es werden nun immer zwei Abschnitte zu einem Abschnitt zusammengefasst und dabei sortiert.
In meinem Beispiel unten werden die Abschnitte [2] und [53] zu [2, 53] zusammengefasst. Der entstehende neue Bereich ist dann wieder sortiert. Es werden immer die oberen Elemente der beiden Abschnitte verglichen. In dem unten rot markiertem Bereich werden zum Beispiel erst die Werte 2 und 11 verglichen. Da 2 die kleinste der beiden Zahlen ist wird dieses an die erste Stelle des neuen Abschnittes gesetzt. Anschließend werden die Zahlen 53 und 11 verglichen, usw... (also für die Felder im rot markiertem Bereich werden 3 Vergleiche ausgeführt).
Wenn nur noch ein Abschnitt geblieben ist, ist der Algorithmus beendet.
Quick Sort
Beim Quick Sort wird aus der Liste ein Pivot-Element ausgewählt - häufig das mittlere Element. Besitzt eine Liste zum Beispiel 9 Elemente, so wird das 5. Element als Pivot-Element genutzt. Nun "geht man" die Elemente von links nach rechts so lange ab, bis man auf ein Element stößt, das größer/gleich dem Pivot-Element ist. Auch von rechts nach links geht man die Elemente ab, jedoch so lange, bis man ein Element gefunden hat, dass kleiner/gleich dem Pivot-Element ist (die "Ablauf-Indizes" sind hier dargestellt durch die schwarzen Pfeile). Nun tauscht man beide gefundenen Elemente aus und führt dieses Verfahren weiter durch, bis sich der linke und rechte "Ablauf-Index getroffen haben".
Nun sind alle Elemente der Liste links von vom linken Zeiger aus kleiner/gleich, und rechts größer/gleich als das Pivot-Element selber. Das oben beschriebene Verfahren führt man nun rekursiv auch für den linken und rechten Bereich der Liste durch, bis jeder Bereich nur noch aus einem Element besteht, dass zwangsläufig sortiert ist.

Vergleich der Algorithmen
Theoretischer Vergleich
Jeder Sortier-Algorithmus ist in drei Komplexitätsklassen einzuteilen, eine für den besten Fall (Best Case), eine für die durchschnittliche Komplexität (Average Case) und eine für den schlechtesten Fall (Worst Case). Auch wenn der letztere Fall nur selten eintritt, ist dieser nicht komplett zu vermeiden, weshalb man bei zeitkritischen Vorgängen immer vom Worst Case ausgehen muss.
| Verfahren | Komplexitätsklassen | Stabil* | Bemerkung | ||
|---|---|---|---|---|---|
| Best Case | Average Case | Worst Case | |||
| ↓ Primitive Algorithmen ↓ | |||||
| Bubble Sort | O(n) | O(n²) | O(n²) | Ja | Effizient, wenn Liste gut vorsortiert ist |
| Selection Sort | O(n²) | O(n²) | O(n²) | Nein | |
| Insertion Sort | O(n) | O(n²) | O(n²) | Ja | |
| ↓ Komplexe Algorithmen ↓ | |||||
| Heap Sort | O(n * log(n)) | O(n * log(n)) | O(n * log(n)) | Nein | |
| Merge Sort | O(n * log(n)) | O(n * log(n)) | O(n * log(n)) | Ja | |
| Quick Sort | O(n * log(n)) | O(n * log(n)) | O(n²) | Nein | Die Wahrscheinlichkeit für den Worst Case kann gering gehalten werden |
* Stabil heißt, dass die Reihenfolge zweier Objekte mit dem selben Schlüssel nach dem Sortieren die selbe, wie vor dem Sortieren ist
Vergleich mit meinem Vergleichs-Skript
Ich habe das Vergleichs-Skript auf meinem Windows 10 Rechner (Intel Core i7-6650U mit 2,20GHz) ausgeführt. Die konkreten Ergebnisse sind stark abhängig von der Hardware, und der Auslastung des Systems (usw...), sodass diese nicht direkt vergleichbar sind. Interessant sind in erster Linie die Verhältnisse der verschiedenen Algorithmen.
Die Tabelle mit den konkreten Ergebnissen (Zeitangabe in Sekunden, und Anteil gegenüber dem maximalen Wert der Zeile) findest du ganz unten im Artikel. Nicht jede Zelle ist gefüllt, da je nach Algorithmus und Anzahl der zu sortierenden Objekte der Vorgang mehrere Jahre gedauert hätte...
Beim Betrachten der Tabelle am Ende der Seite fallen zwei Punkte direkt ins Auge:
Punkt eins ist, dass sich die Laufzeiten für eine geringe Anzahl an Elementen (bis ca. 26 = 64 Elemente) nur wenig unterscheiden - es macht in dieser Größenordnung also keinen großen Unterschied, welches der Verfahren genutzt wird. Bei noch weniger Elementen (bis ca. 23 = 8 Elementen) sind häufig sogar die primitiven Sortier-Verfahren mit einer Komplexitätsklasse von O(n²) effizienter, da nur sehr wenig Aufwand "für die Logik drum herum" benötigt wird (fixe Zahlen als Präfix, zB 20 * n log(n)). Daher gibt es sgn. Hybrid-Verfahren, die primitive und komplexe Sortier-Verfahren kombinieren. Beispielsweise wird mit dem Quick Sort-Verfahren die Menge an zu sortierenden Elementen immer weiter reduziert (durch das divide and conquer-Verfahren), sodass die entstehenden Teilmengen mit nur wenig Elementen schließlich mit dem Bubble Sort sortiert werden.
In der Tabelle unten sind die resultierenden Laufzeiten für 21 bis 26 Elemente für zwei Algorithmen mit den Komplexitäten 20*n*log(n) bzw. n² eingetragen. Es fällt auf, dass der Algorithmus mit der höheren Komplexitätsklasse O(n²) wenige Elemente schneller sortiert, als der Algorithmus mit der niedrigeren Komplexitätsklasse O(n log(n)).
| 2^1 = 2 | 2^2 = 4 | 2^3 = 8 | 2^4 = 16 | 2^5 = 32 | 2^6 = 64 | |
|---|---|---|---|---|---|---|
| 20 * n log(n) | 12 | 48 | 144 | 385 | 963 | 2.312 |
| n² | 4 | 16 | 64 | 256 | 1.024 | 4.096 |
Die Unterschiede in der Effizienz der Algorithmen fallen erst bei deutlich mehr Elementen auf - zum Beispiel bei 214 (16.384) Elementen (blau markierte Zeile). Für diese Menge an Elementen benötigt der primitive Insertion Sort-Algorithmus ca. 42 Sekunden, während der komplexe Quicksort Algorithmus weniger als 0,2 Sekunden benötigt - also ein gewaltiger Unterschied. Bei noch mehr Elementen würde die Differenz noch stärker zunehmen.
Zusammenfassung
Sortier-Algorithmen werden überall im Alltag eingesetzt - auch wenn man sie nicht direkt sieht. Egal ob im Dateimanager, bei einer Google-Suche, oder beim Entsperren eines Smartphones. Überall kommen solche Verfahren zum Einsatz.
Wenn nur kleine Datenmengen sortiert werden sollen wird normal nur wenig Rechenzeit benötigt und es ist relativ irrelevant, welches Sortier-Verfahren verwendet wird. Wenn aber die Menge an zu sortierenden Elementen größer wird, merkt man relativ zügig, dass der verwendete Algorithmus von erheblicher Bedeutung ist. Dies ist der Grund dafür, dass es eine große Menge an Algorithmen gibt, die entweder für den allgemeinen Gebrauch entworfen wurden, oder für genau ein Problem konzipiert wurden.
Mittlerweile sind die Algorithmen so weit entwickelt, dass die bestmögliche Komplexitätsklasse O(n log(n)) erreicht wird, und die Algorithmen nicht mehr wesentlich beschleunigt werden können.
Weitere Links
- Python Sorting Algorithms auf github.com
- Interessante Wikipedia-Artikel
- Gegenüberstellung einiger Sortier-Algorithmen auf youtube
Tabelle mit Test-Ergebnissen
| Elemente | Bubble Sort | Selection Sort | Insertion Sort | Heap Sort | Merge Sort | Quick Sort |
|---|---|---|---|---|---|---|
| 25 =32 |
0,0010s (100%) |
0,0010s (100%) |
0,0001s (10%) |
0,0005s (55%) |
0,0004s (46%) |
0,0005s (54%) |
| 26 =64 |
0,0014s (97%) |
0,0015s (100%) |
0,0005s (33%) |
0,0005s (33%) |
0,0005s (33%) |
0,0000s (0%) |
| 27 =128 |
0,0065s (100%) |
0,0050s (77%) |
0,0040s (62%) |
0,0030s (46%) |
0,0010s (15%) |
0,0010s (15%) |
| 28 =256 |
0,0321s (100%) |
0,0281s (88%) |
0,0115s (36%) |
0,0035s (11%) |
0,0026s (8%) |
0,0020s (6%) |
| 29 =512 |
0,1079s (100%) |
0,0782s (72%) |
0,0422s (39%) |
0,0060s (6%) |
0,0040s (4%) |
0,0030s (3%) |
| 210 =1024 |
0,4824s (100%) |
0,3410s (71%) |
0,1660s (34%) |
0,0211s (4%) |
0,0140s (3%) |
0,0120s (2%) |
| 211 =2048 |
1,6963s (100%) |
1,2593s (74%) |
0,6628s (39%) |
0,0320s (2%) |
0,0216s (1%) |
0,0191s (1%) |
| 212 =4096 |
6,5789s (100%) |
5,0763s (77%) |
2,8863s (44%) |
0,0697s (1%) |
0,0476s (1%) |
0,08003s (0,4%) |
| 213 =8192 |
20,810s (100%) |
10,693s (51%) |
0,1469s (1%) |
0,0952s (0,5%) |
0,0803s (0,4%) |
|
| 214 =16.384 |
42,550s (100%) |
0,3295s (0,8%) |
0,2086s (0,5%) |
0,1795s (0,4%) |
||
| 215 =32.768 |
0,7227s (100%) |
0,4693s (65%) |
0,4018s (56%) |
|||
| 216 =65.536 |
1,5775s (100%) |
1,0237s (65%) |
0,9712s (62%) |
|||
| 217 =131.072 |
3,7187s (100%) |
2,3508s (63%) |
1,7352s (47%) |
|||
| 218 =262.144 |
7,7554s (100%) |
5,2373s (68%) |
3,8925s (50%) |
|||
| 219 =524.288 |
17,558s (100%) |
11,389s (65%) |
8,3373s (48%) |
|||
| 220 =1.048.576 |
24,912s (100%) |
17,5712s (71%) |
||||
| 221 =2.097.152 |
53,311s (100%) |
35,578s (67%) |
||||
| 222 =4.194.304 |
116,41s (100%) |
81,926s (70%) |